In this tutorial, I am going to discuss the followings:

1. the necessary steps of building a convolution neural network (CNN) model in PyTorch,
2. how to calculate the spatial dimension (height and width) of the output of a convolution layer (it will be useful for resolving size mismatch errors when designing a CNN model),
3. the dimensions of the filters in a convolution layer,
4. the number of parameters of a CNN model.

When discussing CNN model, the terms kernel and filter are often used interchangeably. However, in this tutorial, I am going to make a distinction between them. I will adopt the convention that a filter is a stack of kernels. Kernel is 2-d and its dimension is height \(\times\) width. Filter is 3-d and its dimension is height \(\times\) width \(\times\) depth.

This tutorial is meant to be straight forward and focused only on buiding a CNN model (but not how to train it), and hopefully in the end you will be able to implement any CNN model in PyTorch with ease.

1. Building a CNN

In PyTorch, we build a CNN model by creating a subclass of torch.NN.Module. I am not going to discuss what exactly torch.NN.Module is. For now, I think it is sufficient to say that it is the base class of all neural network models built in PyTorch.

In the definition of this subclass (let’s call it myCNN), we must implement two of its method: __init__() and forward().

import torch
import torch.nn as nn
import torch.nn.functional as F

class myCNN(nn.Module):
    def __init__(self):
        super().__init__()
	#convolution layer 1
        self.conv1 = nn.Conv2d(3, 16, kernel_size=3, stride=2, padding=1)
	#convolution layer 2
        self.conv2 = nn.Conv2d(16, 32, kernel_size=3, stride=2, padding=1)
	#fully-connected layer
        self.fc = nn.Linear(32*8*8,10)
        
    def forward(self, x):
        x = x.view(-1, 3, 32, 32) #(batch size, channels, height, width)
        x = F.relu(self.conv1(x))
        x = F.relu(self.conv2(x))
        
        #convert x to a 1-d vector 
        size = x.size()[1:]  #all dimensions except the batch dimension
        num_features = 1
        for s in size:
            num_features *= s        
        x = x.view(-1, num_features)
        
        x = self.fc(x)
        
        return x

In __init__(), we define the layers. In this example, the network has 2 convolution layers, and one fully-connected layer.

In forward(), we specify how to stack the layers and how an input image is passed along the network. This is where we specify the activation fucntion for each convolution layer. In Fig. 1, it depicts a foward pass of an image input to this network.

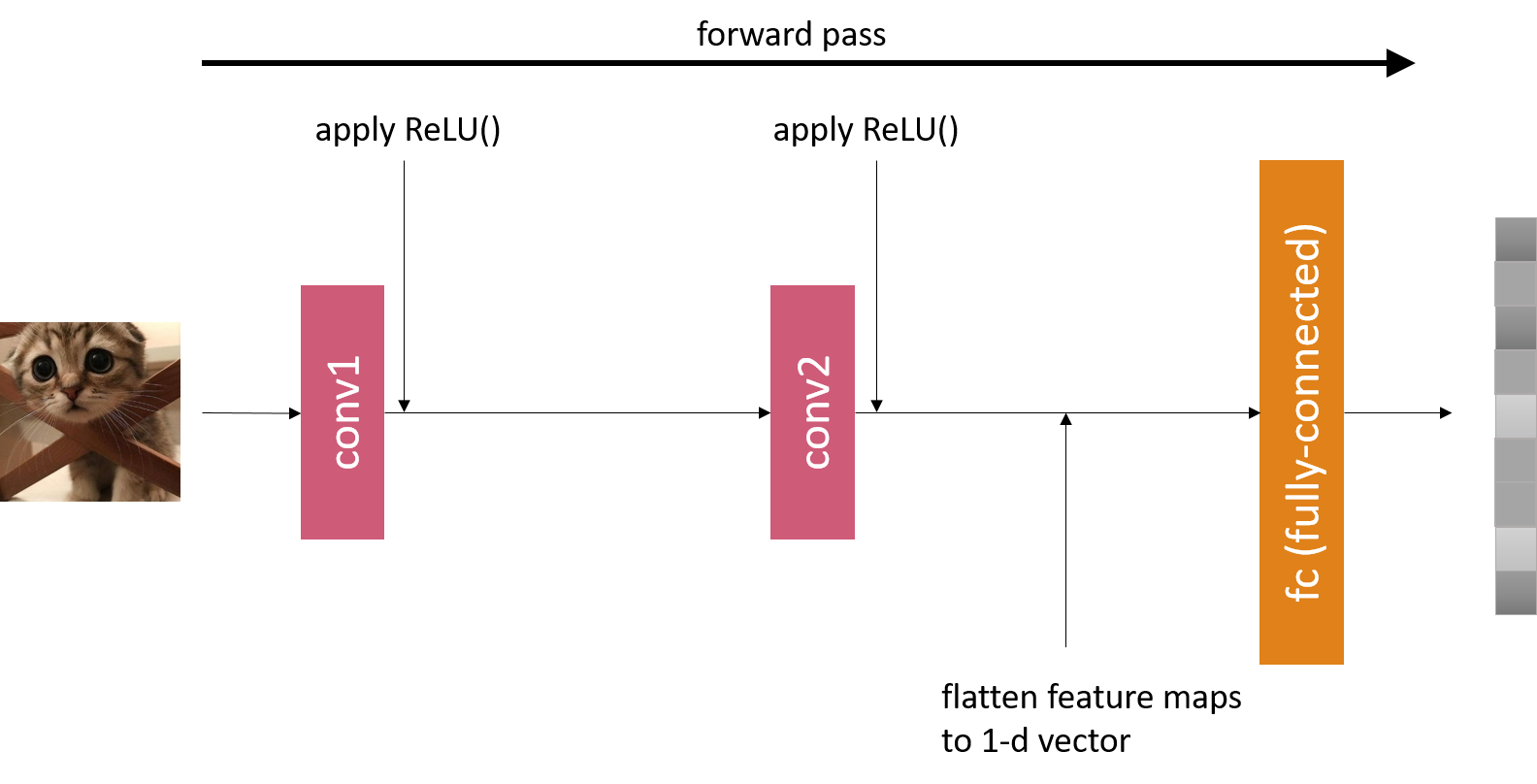
If we create an instance from this class, it will give us a CNN model with the specified structure.

cnn = myCNN()
print(cnn)

> myCNN(
	(conv1): Conv2d(3, 16, kernel_size=(3, 3), stride=(2, 2), padding=(1, 1))
	(conv2): Conv2d(16, 32, kernel_size=(3, 3), stride=(2, 2), padding=(1, 1))
	(fc): Linear(in_features=2048, out_features=10, bias=True)
  )

We can then input an image by calling the model itself or using forward().

ip = torch.randn(1, 3, 32, 32)
out = cnn(ip)
print(out)
out2 = cnn.forward(ip)
print(out2)

> tensor([[-0.0810,  0.0143,  0.0658,  0.0611,  0.1605,  0.0042, -0.0662,  0.0746,
	0.1831,  0.1606]], grad_fn=<AddmmBackward>)
> tensor([[-0.0810,  0.0143,  0.0658,  0.0611,  0.1605,  0.0042, -0.0662,  0.0746,
	0.1831,  0.1606]], grad_fn=<AddmmBackward>)

And this is all you need to do to build a CNN model using PyTorch.

2. Kernel Size and the Spatial Dimension of the Convolution Layer Output

If we instead set the kernel sizes of both convolution layers to 5, and again input an image of size \(32 \times 32\), it is going to give us an error.

#Replace with these lines in the definition of myCNN
self.conv1 = nn.Conv2d(3, 16, kernel_size=5, stride=2, padding=1)
self.conv2 = nn.Conv2d(16, 32, kernel_size=5, stride=2, padding=1)

ip = torch.randn(1, 3, 32, 32)
out = cnn(ip)

> RuntimeError: size mismatch, m1: [1 x 1568], m2: [2048 x 10]

This is because the fully-connected layer at the end of the model is expecting a different input size.

How to calculate the height and width of the convolution layer output

The height and width \((H_{\text{out}}, W_{\text{out}})\) of the output of a convolution layer, given the height and width of the input \((H_{\text{in}}, W_{\text{in}})\), can be calculated using this equation:

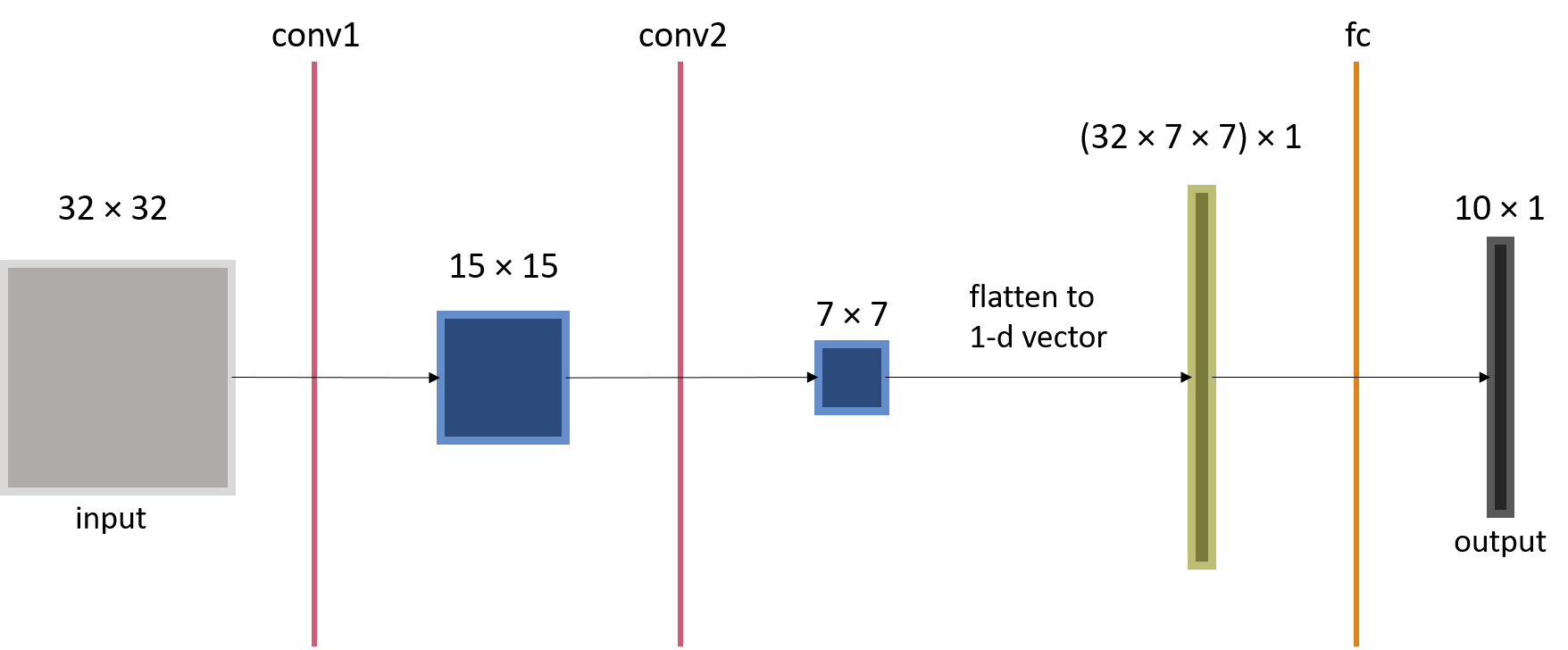
Therefore, for the CNN model in Example 1, if the kernel sizes for both convolution layers are set to 5, then the output of conv2 will have a spatial dimension of \(7 \times 7\). We can then modify the fully-connected layer accordingly.

#Replace with this line in the definition of myCNN
self.fc = nn.Linear(32*7*7,10)

ip = torch.randn(1, 3, 32, 32)
out = cnn(ip)
print(out)

> tensor([[ 0.0236,  0.0631, -0.1651,  0.0212,  0.0478,  0.0933, -0.0332, -0.0417,
	0.0639,  0.0592]], grad_fn=<AddmmBackward>)

In figure 2, it depicts how the spatial dimension of the layer output progresses along a CNN model (when kernel sizes are set to 5).

You may wonder why the input length of the fully-connected layer is set to be \(32 \cdot 7 \cdot 7\). As will be futher explained in the next section, each filter in the convolution layer produces an output of size \(7 \times 7\), and there are 32 such filters which together product a volume of \(32 \times 7 \times 7\). This volume is the flattened to create a 1-d input to the fully-connected layer.

When designing CNN models, it is crucial to know these equations because we often want to try out different kernel sizes. While small kernels can capture local features, large kernels may be able to provide more contextual information as they cover larger areas in the input image.

Another reason we would need these equations is that a CNN model always has a default input size. For example, ResNet has a default size of \(224 \times 224\), and InceptionV3 has a default size of \(299 \times 299\). An input image deviates from the default size is likely to produce a size match error. In that case, you will have to scale or crop it. Alternatively, you can make adjustments to your model layers to fit your input image size.

3. Filter Dimension and Number of Parameters

So far, we have discussed mostly about the kernels. In this section, we are going to look at the filters and see what exactly happens during the convolution.

Volumetric convolution

A filter is a stack of kernels. The depth of the filter (which is the number of stacked kernels) is equal to the number of channels of the input image. As depicted in figure 3, the filter convolves with the entire volume (height \(\times\) width \(\times\) number of channels) of the input to produce one slice of the output, which is also called a feature map.

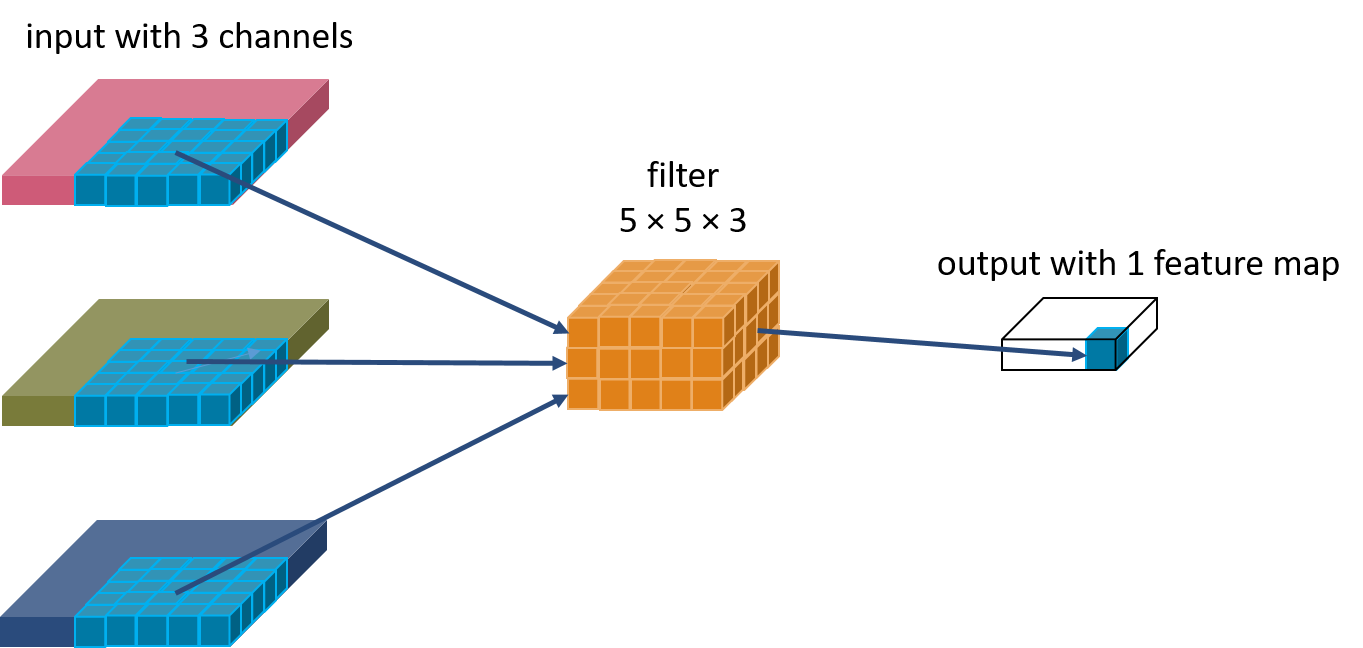
The convolution would result in only one feature map. If we want the output to have multiple feature maps, the layer will need multiple filters. This is depicted in fgiure 4.

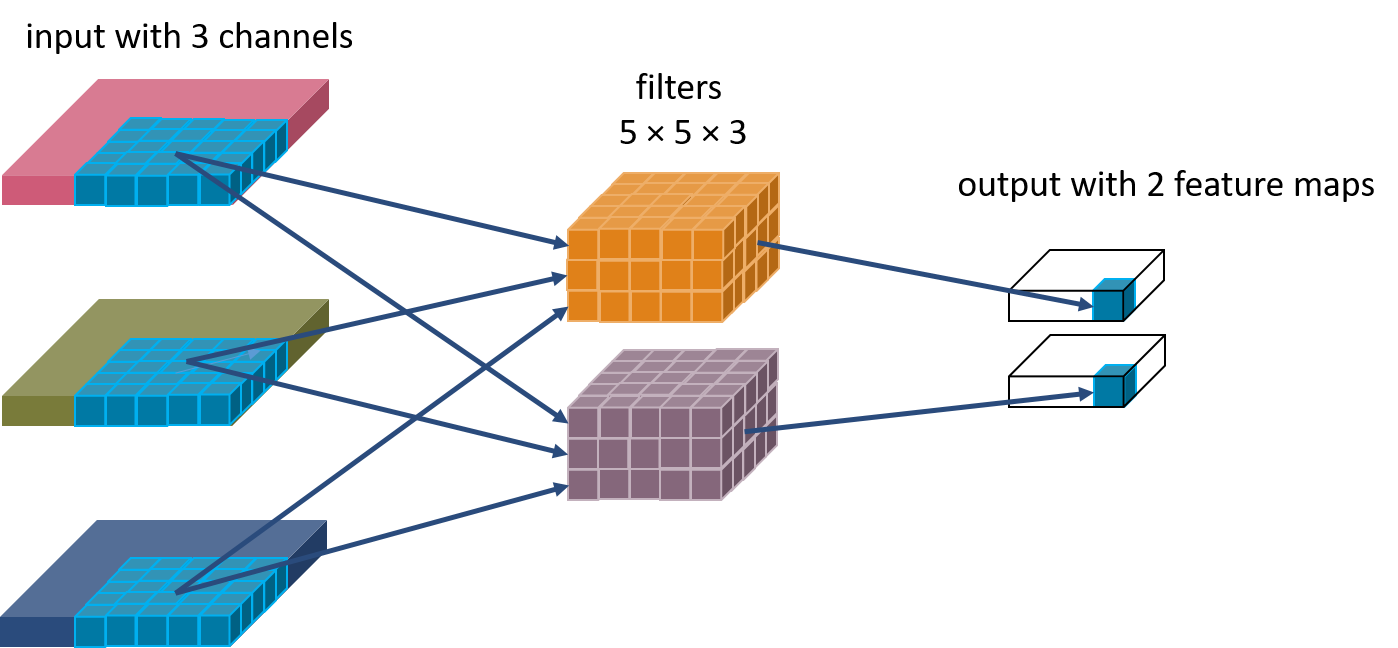
If you want the output to have 32 feature maps, you will need 32 filters in the convolution layer. I hope this gives you a clear picture of what goes through a convolution layer.

Calculating the number of parameters

Finally, we will look at the number of parameters of each layer.

For a convolution layer, the number of parameters is the product between the number of filters and the number of parameters of each filter. In example 1, conv1 has an input with 3 channels and an output with 16 feature maps. Therefore it has 16 \((5 \times 5 \times 3)\) filters, and its number of parameters is 1200. Similarly, conv2 has an input with 16 channels and an output with 32 feature maps. Therefore it has 32 \((5 \times 5 \times 16)\) filters, and its number of parameters is 12800.

For a fully-connected layer, each output is calculated as the dot product of the input and the corresponding weights, then plus a bias.

Therefore, for each output, there are same number of weights as number of input. In our example, fc has 10 output, therefore it has \((32 \times 7 \times 7 + 1)\times 10\) parameters, which is 15690.

The total number of parameters of this CNN model is given by:

This is the end of this very gentle introduction. I hope it would help you gain a better understanding of CNN as well as get started in PyTorch.